
We present a fast method for finding optimal parameters for a low-resolution (threading) force field intended to distinguish correct from incorrect folds for a given protein sequence. In contrast to other methods, the parameterization uses information from >107 misfolded structures as well as a set of native sequence-structure pairs.
In addition to testing the resulting force field's performance on the protein sequence threading problem, results are shown that characterize the number of parameters necessary for effective structure recognition.
Keywords: fold recognition; low-resolution force field; optimization algorithm; parameter determination; threading
Currently, there is no shortage of low-resolution, protein fold recognition force fields (Lemer et al., 1995; Sippl, 1995; Böhm, 1996; Jernigan & Bahar, 1996; Jones & Thornton, 1996; Sippl & Flöckner, 1996; Torda, 1997). These are nearly all designed to tackle the threading problem, where a sequence is tested for compatibility with a series of structures and a pseudo-potential energy function is applied to find the most appropriate structure for some sequence.
It is not known whether a protein's fold can be explained simply by internal interactions or whether it is the result of complex interplay with the environment and folding history. Consequently, the optimal fold recognition function may not need to be based on real physical properties. Instead, it may simply reflect some common denominator among naturally expressed proteins (and solved structures).
Originally, it was seen as an achievement for a method to be able to recognize a sequence's native structure from a large number of wrong, decoy structures (Bowie et al., 1991; Jones et al., 1992). Since then, the problem of self-recognition seems to have become a minimal requirement (Defay & Cohen, 1996; Jones & Thornton, 1996). With this baseline, a new force field is probably only interesting if there is evidence of remarkable performance or some cunning innovation. The work here may not satisfy either of these criteria, but it does have some interesting properties. There is no reliance on Boltzmann statistics (Jones et al., 1992) nor on any obvious physics. Rather than merely aim for self-recognition, the methodology optimizes the statistical significance of such recognition. This is based on the philosophy of defining a criterion for force field quality and then adjusting parameters to optimize this property (Seetharamulu & Crippen, 1991; Maiorov & Crippen, 1992; Hao & Scheraga, 1996; Koretke et al., 1996; Mirny & Shakhnovich, 1996; Ulrich et al., 1997). Next, the parameterization scheme includes the effect of structures generated by threading. Unlike earlier work (Ulrich et al., 1997), a tractable scheme has been devised whereby one can easily handle parameterization with more than 300 native structures and 107 misfolded alternative structures. Most importantly, the force field functional forms were chosen so that one could guarantee convergence using simple gradient-based optimization. Finally, the method was applied to give some estimate of the force field's "learning capacity," or the appropriate number of adjustable parameters. This work is also based on a fundamentally unusual approach to the general problem of protein fold recognition. The work here is intended to produce a force field that only applies to native-like structures and is optimized for that purpose. This means that one accepts at the outset that it may not be the best method for sequence-structure alignment calculations and should be tested only on ungapped alignments. A separate and specifically optimized force field will be used for gapped alignments (unpubl. results).
Each amino acid was represented by five interaction
sites. Four of these were at backbone atom positions (N,
Calpha, C, and O) and one at the position of
the Cbeta carbon. For glycine residues, an
interaction site was positioned at the location of a fictitious
Cbeta atom calculated assuming ideal geometry.
The total energy of a chain of length N
was the sum of pairwise interactions between all atoms
and a solvent/environment energy of each residue based
only on the Calpha atom position:

where i and j are indices running over the five interaction sites in each residue and k runs over the set of Calpha atoms.
The pair interaction energy E(i,j)
between two atoms i and j
depended on spatial distance dij,
topological distance sij
in the amino acid sequence, and the atom types ti
and tj.
A simple sigmoidal function was chosen to describe atom
pair interactions:
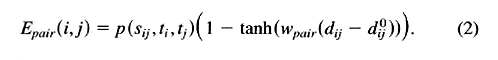
The parameters p(sij,ti,tj) determine the interaction strength and were chosen such that native sequence-structure pairs would be optimally discriminated from non-native alternative combinations. The parameters dij0 and wpair control the step position and slope of the function and were based on crude database statistics. To reduce the total number of parameters, interactions did not depend on chain direction, so p(sij,ti,tj) = p(sij,tj,ti), and only three classes of topological distances were distinguished: i -> j = i + 2, i -> j = i + 3, and i -> j >= i + 4. Each class was treated separately with different sets of parameters. Adjacent (i -> j = i + 1) residues were not treated explicitly in the interaction function.
The force field was based on 24 atom types. These were four backbone atoms, N, Calpha, C, and O, and 20 different Cbeta atoms, depending on the amino acid type. This meant that, for a given topological distance, there were {24(24 + 1)}/2 = 300 interaction types.
The second term in Equation
1 was a single residue contribution depending
on the Calpha environment of each residue. One
could see this as analogous to a solvent interaction contribution,
but it was not parameterized as such and will also include
general, nonspecific environment contributions. For simplicity
and consistency, the same functional form as for pair interactions
was used:

where ai is the amino acid type, n(i) is the number amino acids separated by more than three amino acids in the sequence with a Calpha carbon within 5.8 Å of Cijalpha. The constant n0 was set to 3, approximately the average of n(i) over all amino acid types.
This resulted in a total of 920 parameters to adjust [300 pair interaction parameters p(sij,ti,tj) per class of topological distance sij and 20 atom parameters p(ai)]. In addition, a total of 47 nonadjustable parameters were used (15 dij0 parameters per topological distance and two parameters wpair and wsol determining the function slopes).
Given a functional form for the discrimination function,
one wants a set of parameters that optimally discriminate
native from alternative sequence-structure combinations.
If one assumes that the energies for one sequence on all
possible nongapped alignments are Gaussian distributed,
the normalization factor (z-score)
describes the relative position of the native state relative
to the distribution of all states:

E denotes the energy of an alternative structure, Enat is the energy of a native structure, and the brackets < > denote the arithmetic average over all configurations.
In a similar vein to the idea of Koretke et al. (1996) and Hao and Scheraga (1996), the functional forms, Equations 2 and Equation 3, were chosen such that
energy was linearly dependent on p(v),
a scaling parameter dependent on the interaction type v.
v, in turn, was given by the switching
function:

Using this definition, an energy calculation is equivalent
to the evaluation of a scalar product of a parameter vector
vector(P) and a vector vector(X)(vector(R), vector(S)) depending on
both coordinates vector(R) and sequence vector(S):

The dimension of the vectors was given by the number of
adjustable parameters n, and the vectors
were defined as

Thus, the average alternative energy is given by

where vector(R)nat and vector(S)nat refer to the native coordinates and sequence.
The average energy squared can be re-written as the
sum over all elements of the Hadamard product of the matrices
_P_ and _X_(vector(R),
vector(S)):

with <DeltaxiDeltaxj>
the covariance elements:
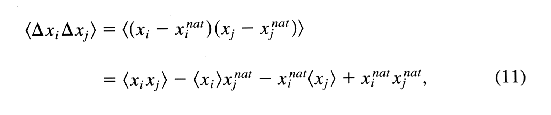
where xi denotes the ith element in vector(X)(vector(R), vector(S)) and pi is denoted the ith element in vector(P).
The goal of the parameter adjustment was to optimize
the discrimination power of the force field or, in other
words, to obtain the most negative z-scores
(Equation 4) for
proteins in the calibration set. In order to find the parameter
vector that optimally discriminates nlib
native protein structures in the calibration set from alternative
structures, the target function t
was constructed as a weighted average of individual protein
z-scores zi:
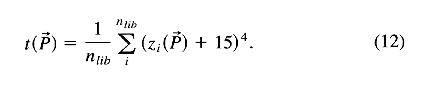
This target function can be seen as a direct measure of force field quality or capability. The fourth power was an arbitrary choice, sharply penalizing non-native conformations. The constant of 15 could be seen as a target level and should be as large as possible. The value was determined by trial and error. The target function was minimized, with respect to force field parameters, by a quasi-Newton method (Shanno & Puha, 1976). This kind of local minimization assumes that there is only one local minimum with respect to parameters. It was not proven rigorously, but the same result was achieved from five different, random start configurations of vector(P). This target function is preferred to an arithmetic average of z-scores because proteins with z-scores closer to zero are given a higher weight and a better discrimination ability can be achieved.
A minimization algorithm such as the one used in this work may require hundreds of function evaluations of Equation 12 to converge. This means one has to recalculate the z-score for each protein in the calibration set at every step parameter optimization. The most expensive aspect of this would be those properties (averages) that depend on the large number of alternate, incorrect structures. In practice, the averages given by Equations 9 and Equation 10 are independent of the parameters and need be calculated only once at the start of an optimization. This results in a remarkably swift method for force field parameterization.
In order to test the effect of the number of parameters on force field performance, a series of parameterization calculations were done. At each step, the parameters were grouped using a standard cluster analysis algorithm, allowing the creation of an arbitrary number of class interaction types.
Given a set of such classes, the parameterization could be repeated, resulting in a new force field with fewer parameters.
The clustering algorithm was the single linkage method (Massart & Kaufmann, 1983) and was applied within each set of parameters for a single topological distance. Thus, for example, long-range parameters were not grouped with short-range parameters.
Two different measures of force field performance were used:
The z-score of each native structure in the ensemble of alternative structures.
The correlation between energy and distance matrix error (DME) (Havel, 1990).

where dij is the distance between Calpha atoms i and j in one conformation and d'ij is the corresponding distance in the second structure.
Force fields were tested using two different protein sets.
The calibration/parameterization set, used in the optimization of parameters. This is a test of recall.
The test set with only low sequence homology to proteins in the calibration/parameterization set. This is a test of generalization.
The purpose of the first data set was to investigate the "learning capacity" of the force field and test whether the functional forms and the parameterization process are suitable. The second set tested the ability to generalize to unknown data and decide whether the force field reflected general protein structure information or was merely over-fitting to the data. Over-fitting would occur if the number of parameters was large relative to the information content of the training data.
For parameterization and analysis, we used a large number of alternative conformations to define a "reference state." These alternative structures were assumed to be "protein-like" and to reproduce an ensemble of important conformations. Using fragments from known database structures guarantees protein-like conformations in that alternative conformations will have regular secondary structure, proper backbone torsion angle distributions, and will not suffer from steric overlap. Although it is not guaranteed, the alternative structures will often be as compact as native structures. Because less compact structures were not included in the parameterization, the force field may be weak at discriminating native conformations from partly unfolded or otherwise non-native structures.
The analysis of force field capability is largely based on z-scores, which assumes a Gaussian distribution of energies of alternative, misfolded structures. Figure 1A, B, C, and D shows this distribution for the alternative structures for two example proteins. The figure also shows a semi-logarithmic plot and the fit to the expected quadratic function.
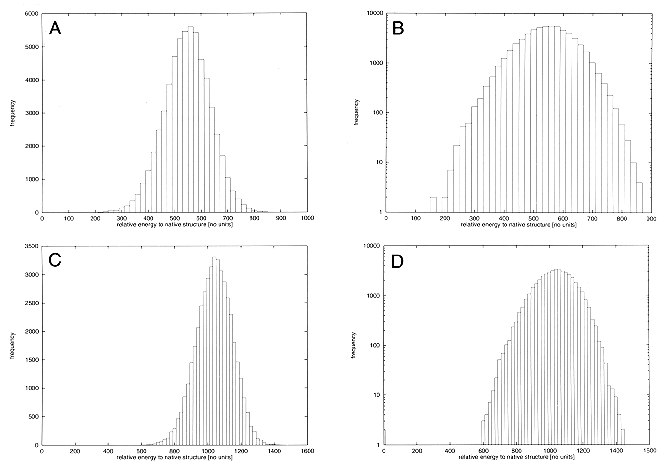
Fig. 1
Energy distribution of alternative conformations
relative to energy of native structure.
A: Protein 1etc_. B:
Protein 1etc_, semilogarithmic plot. C:
Protein 1aep_. D: Protein 1aep_, semi-logarithmic
plot.
Figure 2A and B shows the force field's performance for each structure in the calibration/parameterization set and in the test set.

Fig. 2
z-Scores versus protein
chain length. A:
Calibration/parameterization set. B:
Test set.
The z-score for each native sequence-structure pair is shown as a function of protein size. Few proteins larger than 100 amino acid have a z-score higher than -5, showing high statistical confidence in the ability of the force field to pick the correct fold from all alternative structures. For smaller proteins, the z-score is closer to zero, meaning that one can have little confidence in predictions. This trend may be due to the larger number of (discriminative) interactions in larger molecules. It is also possible that small proteins with a relative large surface area suffer from the force field's crude accounting for solvent effects. At the same time, this trend is probably exaggerated by the smaller number of alternative structures for larger proteins. Because a sequence can only be threaded onto proteins at least as large, there are simply fewer alternatives for larger structures. The poorer performance of the force field with small proteins may also be due to the nature of these proteins. Many small proteins are expressed with large pro-regions that are cleaved after folding and many contain a large number of disulfide bridges, which may force the sequence into otherwise energetically nonoptimal structures.
Despite a different protein size distribution in parameterization set and test set, the z-score results of the two different sets are very similar. This is promising for structure prediction, because the test set is unknown to the force field and demonstrates that the force field is able to generalize consistently for more than 300 proteins.
For successful fold recognition, it is necessary to recognize native folds and very desirable to recognize folds that are geometrically near the native. This is difficult to show in general, but an example was constructed for the trypsin fold motif. A fold library was constructed containing 103 trypsin-related proteins taken from the FSSP library (Holm & Sander, 1994) in addition to the calibration/parameterization set of proteins. This meant that a large number of similar decoy structures could be generated, as well as the alternative structures that would be available from the calibration/parameterization library. The test sequence was from beta-trypsin (PDB acquisition code 1tpo), and 30,125 alternative structures were tested.
For each alternative structure, the difference from the native was measured using the DME of Equation 13 and, ideally, the force field should produce results such that alternative structures that are near to the native (low DME) are of lower energy than those very different to the native. One would expect high dispersion of energies at high DME, but at least one would want a funnel-like relationship (Bryngelson et al., 1995; Onuchic et al., 1995).
Figure 3 displays the extent to which this scoring function produces a funnel-like relation.
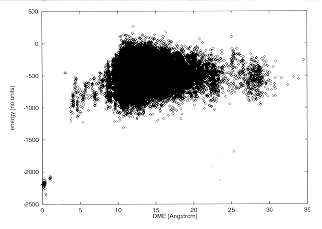
Fig. 3
Force field energies versus DME for beta-trypsin.
The native sequence was threaded onto 30,125 structures.
When the structures are highly similar to trypsin (DME <= 1 Å), the energies are close to the native energy and well separated from the energy distribution of alternative structures. In this case, the fold can be recognized correctly. The limit of recognition seems to be near 4 Å when the energy of correct folds becomes too close to incorrect folds.
The number of parameters is a crucial point in any data-fitting exercise. A certain number of parameters is necessary to fit the general features of the data, but the number of parameters should be kept small to avoid over-fitting. In the case of fitting parameters for fold recognition force fields, literature estimates of the approximate number of parameters span the range from less than ten (Sun et al., 1995; Thomas & Dill, 1996) to tens of thousands (Hendlich et al., 1990; Jones & Thornton, 1993). We tried to explore the lower limit of the number of parameters in our fold recognition force field. Although the appropriate number of parameters depends on the functional forms used for interaction function, our results may be some upper limit because our interaction functions were so simple. Figure 4 summarizes the results of force field parameterization with different numbers of parameter classes.
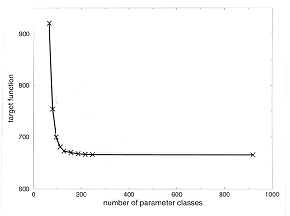
Fig. 4
Target function as a function of the number
of parameter classes in the parameterization process.
When reducing the number of classes from initial 920 to 127, the target function (Equation 12) of the parameterization hardly changes. With further clustering of classes to below approximately equal to100 parameters, there is a rapid increase of the target function and significant deterioration of quality of the fit.
Ideally, the number of parameters should reflect some number of underlying degrees of freedom in the data. Unfortunately, this is an unknown quantity. It is then especially interesting to compare these results with Thomas and Dill (1996). Using different functional forms and a smaller test set, they suggested there was no benefit in using more than 10 amino acid types. Ultimately, a more direct comparison would be useful.
This functional form was chosen for several reasons. First, it is sufficient to distinguish two states and similar "contact potential terms" have a successful history in protein fold prediction (Tanaka & Scheraga, 1976; Miyazawa & Jernigan, 1985) and lattice simulations (Lau & Dill, 1989; Shakhnovich & Gutin, 1989, 1990). Second, the use of a continuous form with a defined derivative with respect to parameters allows the use of efficient minimization methods. Last, the form does not have a narrow range of distances that result in low energy, as would be the case with a Lennard-Jones like term (Levitt, 1976; Oobatake & Crippen, 1981). This means that calculated pseudo-energies are less sensitive to perturbations of coordinates and more tolerant of "errors" in geometry, which makes processing of structures to remove strains (Park & Levitt, 1996; Ulrich et al., 1997) unnecessary.
Parameters were optimized using function minimization, which is known to fail if the function hyper-surface is rough and barriers separate local minima. To our surprise, this is not the case with our target function (Equation 12). The hyper-surface turned out to be smooth and function minimization was able to locate a single minimum from five randomly chosen starting configurations of vector(P). As a last check, parameter dynamics simulation on the target function hyper-surface, similar to the method of Ulrich et al. (1997), combined with simulated temperature annealing (Kirkpatrick et al., 1983), was performed. No improvement of the results was obtained.
We used two different measures to assess the quality of the force field. Although these measurements are not completely independent of each other, they give a representative description of the performance of a force field.
The z-score describes the energy of the native or any other single structure relative to an idealized energy distribution of all alternative structures. Therefore, the z-score depends highly on quality of the decoy structures used in the ensemble of alternates.
Analyzing the correlation between energy and DME of misfolded structures avoids this problem. Nevertheless, this measure is not invariant with arbitrary scaling of energies (which does not affect discrimination properties) and therefore requires an additional external energy reference.
The philosophy of this work has been that, by building a force field optimized for discrimination, one should obtain better performance than using a force field that simply reflects structural properties of native structures. Because we find a global minimum to the force field construction problem, one could go so far as to say that this is the best possible force field. Of course, this is only true in the framework of the functional form and with respect to the target function (Equation 12) used.
The parameterization and testing has only been conducted on ungapped alignments and it is likely that the parameter set here is not ideal for calculating sequence-structure alignments. Continuing in this vein of specialized force fields, a different optimization methodology has been used with different functional forms and a different target function for the sequence-structure alignment problem (unpubl. results). This scoring function is only expected to be used, given a reasonable native-like alignment produced by a separate alignment procedure. Hence, this work has been restricted to ungapped alignments (with a very large number of decoys) and testing with common literature measures such as z-scores.
For comparison, the results here have been based on common literature measures such as z-score, and the results cover a large range of proteins. At the same time, the family of native proteins and decoys is probably different from every other in the literature, so a true comparison of force field performance is not really possible and some of the claims in this work remain as unsubstantiated as others in the literature.
The calibration/parameterization set of proteins was taken from Hobohm and Sander (1994), March 1996 release, and consisted of protein chains such that no sequence had more than 25% sequence identity with any other member of the set. From this list, chains of 100 or more residues and with all backbone heavy atoms were selected. This resulted in a set of 370 protein chains in the final calibration set (Table 1).
Table 1. Parameterization protein set (PDB acquisition codes)
A library of misfolded, decoy structures for each protein chain was generated by threading the native sequence onto all structures of the same or larger size in the protein library, resulting in a total of 10.54 million alternative structures for the 370 native structures.
For testing, a second set of 342 proteins was chosen (Table 2), again from the list of Hobohm and Sander (1994), such that no protein had more than 45% sequence identity with any other member or any member of the calibration set. Unlike the calibration set, no criterion was applied for chain length and the test set contained many chains of less than 100 residues. Using threading, there were 5.41·106 alternative, misfolded decoy structures generated for this set.
Table 2. Test protein set (PDB acquisition codes)
Parameters were optimized by minimization of the target function (Equation 12) using the parameterization set of 370 proteins until the energy gradient was smaller than 10-6. After the raw force field with 920 adjustable parameters was obtained, parameters were clustered and new force fields were generated with 65, 80, 95, 112, 127, 157, 187, 217, and 247 distinct parameter classes.
The force field parameters are provided as supplementary material. A program capable of scoring alignments using this force field can be found at ftp://ftp.rsc.anu.edu.au/~torda/README.
Böhm G. 1996. New approaches in molecular structure prediction. Biophys Chem 59:1-32.
Bowie JU, Lüthy R, Eisenberg D. 1991. A method to identify protein sequences that fold into a known three-dimensional structure. Science 253:164-170.
Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. 1995. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins Struct Funct Genet 21:167-195.
Defay TR, Cohen FE. 1996. Multiple sequence information for threading algorithms. J Mol Biol 262:314-323.
Hao MH, Scheraga HA. 1996. How optimization of potential functions affects protein folding. Proc Natl Acad Sci USA 93:4984-4989.
Havel TF. 1990. The sampling properties of some distance geometry algorithms applied to unconstrained polypeptide chains: A study of 1830 independently computed conformations. Biopolymers 29:1565-1585.
Hendlich M, Lackner P, Weitckus S, Flöckner H, Froschauer R, Gottsbacher K, Casari G, Sippl MJ. 1990. Identification of native protein folds among a large number of incorrect models: The calculation of low energy conformations from potentials of mean force. J Mol Biol 216:167-180.
Hobohm U, Sander C. 1994. Enlarged representative set of protein structures. Protein Sci 3:522-524.
Holm L, Sander C. 1994. The fssp database of structurally aligned protein fold families. Nucleic Acids Res 24:206-210.
Jernigan RL, Bahar I. 1996. Structure-derived potentials and protein simulations. Curr Opin Struct Biol 6:195-209.
Jones DT, Taylor WR, Thornton JM. 1992. A new approach to protein fold recognition. Nature 358:86-89.
Jones DT, Thornton JM. 1993. Protein fold recognition. J Comp Aided Mol Design 7:439-456.
Jones DT, Thornton JM. 1996. Potential energy functions for threading. Curr Opin Struct Biol 6:210-216.
Kirkpatrick S, Gelatt CD Jr, Vecchi MP. 1983. Optimization by simulated annealing. Science 220:671-680.
Koretke KK, Luthey-Schulten Z, Wolynes PG. 1996. Self consistently optimized statistical mechanical energy functions for sequence structure alignment. Protein Sci 5:1043-1059.
Lau KF, Dill KA. 1989. A lattice statistical mechanics model of the conformational and sequence spaces of proteins. Macromolecules 22:3986-3997.
Lemer CMR, Rooman MJ, Wodak SJ. 1995. Protein structure prediction by threading methods: Evaluation of current techniques. Proteins Struct Funct Genet 23:337-355.
Levitt M. 1976. A simplified representation of protein conformations for rapid simulation of protein folding. J Mol Biol 104:59-107.
Maiorov VN, Crippen GM. 1992. Contact potential that recognizes the correct fold of globular proteins. J Mol Biol 227:876-888.
Massart DL, Kaufmann L. 1983. The interpretation of analytical chemical data by the use of cluster analysis. New York: John Wiley & Sons.
Mirny LA, Shakhnovich EI. 1996. How to derive a protein folding potential? A new approach to an old problem. J Mol Biol 264:1164-1179.
Miyazawa S, Jernigan RL. 1985. Estimation of effective interresidue contact energies from protein crystal structures: Quasi chemical approximation. Macromolecules 18:534-552.
Onuchic JN, Wolynes PG, Luthey-Schulten Z, Socci ND. 1995. Toward an outline of the topography of a realistic protein folding funnel. Proc Natl Acad Sci USA 92:3626-3630.
Oobatake M, Crippen GM. 1981. Residue-residue potential function for conformational analysis of proteins. J Phys Chem 85:1187-1197.
Park B, Levitt M. 1996. Energy functions that discriminate X-ray and near-native folds from well-constructed decoys. J Mol Biol 258:367-392.
Seetharamulu P, Crippen GM. 1991. A potential function for protein folding. J Math Chem 6:91-110.
Shakhnovich EI, Gutin AM. 1989. Formation of unique structure in polypeptide chains. Theoretical investigation with the aid of a replica approach. Biophys Chem 34:187-199.
Shakhnovich EI, Gutin AM. 1990. Enumeration of all compact conformations of copolymers with random sequence of links. J Chem Phys 93:5967-5971.
Shanno DF, Puha KH. 1976. Minimization of unconstrained multivariate functions. AC MTOMS 2:87-94.
Sippl MJ. 1995. Knowledge-based potentials for proteins. Curr Opin Struct Biol 5:229-235.
Sippl MJ, Flöckner H. 1996. Threading thrills and threats. Structure 4:15-19.
Sun S, Thomas PD, Dill KA. 1995. A simple protein folding algorithm using a binary code and secondary structure constraints. Protein Eng 8:769-778.
Tanaka S, Scheraga HA. 1976. Medium- and long-range interaction parameters between amino acids for predicting three dimensional structures of proteins. Macromolecules 9:945-950.
Thomas PD, Dill KA. 1996. An iterative method for extracting energy-like quantities from protein structures. Proc Natl Acad Sci USA 93:11628-11633.
Torda AE. 1997. Perspectives on protein fold recognition. Curr Opin Struct Biol 7:200-205.
Ulrich P, Scott WRP, van Gunsteren WF, Torda AE. 1997. Protein structure prediction force fields: Parametrization with quasi newtonian dynamics. Proteins Struct Funct Genet 27:367-384.